O conjunto A é chamado de domínio da função, enquanto que o conjunto B é denominado de contradomínio da função. São casos particulares de função afim as funções lineares e constante.
Linear: Uma função definida por f: R→R chama-se linear quando existe uma constante a ∈ R tal que f(x) = ax para todo x ∈ R. A lei que define uma função linear é a seguinte:
Linear: Uma função definida por f: R→R chama-se linear quando existe uma constante a ∈ R tal que f(x) = ax para todo x ∈ R. A lei que define uma função linear é a seguinte:
Constante: Uma função definida por f: R→R chama-se constante quando existe uma constante b R tal que f(x) = b para todo x ∈ R. A lei que define uma função constante é:
Gráfico
O gráfico de uma função polinomial do 1º grau, y = ax + b, com a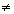
0, é uma reta oblíqua aos eixos Ox e Oy. Esse gráfico é obtido representado-se dois pontos distintos de f e trançando-se a reta por eles.
Gráfico
O gráfico de uma função polinomial do 1º grau, y = ax + b, com a
0, é uma reta oblíqua aos eixos Ox e Oy. Esse gráfico é obtido representado-se dois pontos distintos de f e trançando-se a reta por eles.
Raiz da Função
Estudo do sinal: Crescimento e Decrescimento
O modelo de função afim possui como representação gráfica a figura de uma reta, portanto, as relações entre os valores do domínio e da imagem crescem ou decrescem de acordo com o valor do coeficiente a. Se o coeficiente possui sinal positivo, a função é crescente, e caso ele tenha sinal negativo, a função é decrescente.
Na função crescente, à medida que os valores de x aumentam, os valores de y também aumentam; ou, à medida que os valores de x diminuem, os valores de y diminuem. Já no caso da função decrescente, à medida que os valores de x aumentam, os valores de y diminuem; ou, à medida que os valores de x diminuem, os valores de y aumentam
Chama-se zero ou raiz da função polinomial do 1º grau f(x) = ax + b, a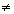0, o número real x tal que f(x) = 0.
0, o número real x tal que f(x) = 0.
EX: f(x) = 2x-6
f(x) = 0
2x = 6
x=3
f(x) = 0
2x = 6
x=3
Estudo do sinal: Crescimento e Decrescimento
O modelo de função afim possui como representação gráfica a figura de uma reta, portanto, as relações entre os valores do domínio e da imagem crescem ou decrescem de acordo com o valor do coeficiente a. Se o coeficiente possui sinal positivo, a função é crescente, e caso ele tenha sinal negativo, a função é decrescente.
Na função crescente, à medida que os valores de x aumentam, os valores de y também aumentam; ou, à medida que os valores de x diminuem, os valores de y diminuem. Já no caso da função decrescente, à medida que os valores de x aumentam, os valores de y diminuem; ou, à medida que os valores de x diminuem, os valores de y aumentam
EX: Estudo do sinal da função f(x) = 3x - 15
f(x) = 3x - 15
3x-15 = 0
x = 15/3
x = 5
f(x) = 3x - 15
3x-15 = 0
x = 15/3
x = 5
A função possui o coeficiente a = 3, no caso maior que zero, portanto, a função é crescente.
Inequação
Uma inequação do 1° grau na incógnita x é qualquer expressão do 1° grau que pode ser escrita numa das seguintes formas:
ax + b > 0;
ax + b < 0;
ax + b ≥ 0;
ax + b ≤ 0.
ax + b < 0;
ax + b ≥ 0;
ax + b ≤ 0.
Onde a, b são números reais com a ≠ 0.
Uma maneira simples de resolver uma inequação do 1° grau é isolarmos a incógnita x em um dos membros.
EX: -2x + 7 > 0
-2x > -7 . (-1)
2x < 7
-2x > -7 . (-1)
2x < 7
x < 7/2
Portanto a solução da inequação é x < 7/2.
Outra forma de resolução da inequação é por meio do estudo do sinal de uma função do 1° grau, com o seguinte procedimento:
1. Iguala-se a expressão ax + b a zero;
2. Localiza-se a raiz no eixo x;
3. Estuda-se o sinal conforme o caso.
2. Localiza-se a raiz no eixo x;
3. Estuda-se o sinal conforme o caso.
EX: -2x + 7 > 0
-2x + 7 = 0
x = 7/2
x = 7/2
Por: Mariana Melo.
Nenhum comentário:
Postar um comentário