Aplicação dos Logaritmos:
Os logaritmos possuem várias aplicações na Matemática e em diversas áreas do conhecimento, como Física, Biologia, Química, Medicina, Geografia entre outras. Iremos através de exemplos demonstrar a utilização das técnicas de logaritmos na busca de resultados para as variadas situações em questão.
Exemplo 1 – Matemática Financeira
Uma pessoa aplicou a importância de R$ 500,00 numa instituição bancária que paga juros mensais de 3,5%, no regime de juros compostos. Quanto tempo após a aplicação o montante será de R$ 3 500,00?
Resolução:
Nos casos envolvendo a determinação do tempo e juros compostos, a utilização das técnicas de logaritmos é imprescindível.
Fórmula para o cálculo dos juros compostos: M = C * (1 + i)t. De acordo com a situação problema, temos:
M (montante) = 3500
C (capital) = 500
i (taxa) = 3,5% = 0,035
t = ?
M = C * (1 + i)t
3500 = 500 * (1 + 0,035)t
3500/500 = 1,035t
1,035t = 7
Aplicando logaritmo
log 1,035t = log 7
t * log 1,035 = log 7 (utilize tecla log da calculadora científica )
t * 0,0149 = 0,8451
t = 0,8451 / 0,0149
t = 56,7
O montante de R$ 3 500,00 será originado após 56 meses de aplicação.
Exemplo 2 – Geografia
Em uma determinada cidade, a taxa de crescimento populacional é de 3% ao ano, aproximadamente. Em quantos anos a população desta cidade irá dobrar, se a taxa de crescimento continuar a mesma?
População do ano-base = P0
População após um ano = P0 * (1,03) = P1
População após dois anos = P0 * (1,03)2= P2
População após x anos = P0 * (1,03)x = Px
Vamos supor que a população dobrará em relação ao ano-base após x anos, sendo assim, temos:
Px = 2*P0
P0 * (1,03)x = 2 * P0
1,03x = 2
Aplicando logaritmo
log 1,03x = log 2
x * log 1,03 = log2
x * 0,0128 = 0,3010
x = 0,3010 / 0,0128
x = 23,5
A população dobrará em aproximadamente 23,5 anos.
Exemplo 1 – Matemática Financeira
Uma pessoa aplicou a importância de R$ 500,00 numa instituição bancária que paga juros mensais de 3,5%, no regime de juros compostos. Quanto tempo após a aplicação o montante será de R$ 3 500,00?
Resolução:
Nos casos envolvendo a determinação do tempo e juros compostos, a utilização das técnicas de logaritmos é imprescindível.
Fórmula para o cálculo dos juros compostos: M = C * (1 + i)t. De acordo com a situação problema, temos:
M (montante) = 3500
C (capital) = 500
i (taxa) = 3,5% = 0,035
t = ?
M = C * (1 + i)t
3500 = 500 * (1 + 0,035)t
3500/500 = 1,035t
1,035t = 7
Aplicando logaritmo
log 1,035t = log 7
t * log 1,035 = log 7 (utilize tecla log da calculadora científica )
t * 0,0149 = 0,8451
t = 0,8451 / 0,0149
t = 56,7
O montante de R$ 3 500,00 será originado após 56 meses de aplicação.
Exemplo 2 – Geografia
Em uma determinada cidade, a taxa de crescimento populacional é de 3% ao ano, aproximadamente. Em quantos anos a população desta cidade irá dobrar, se a taxa de crescimento continuar a mesma?
População do ano-base = P0
População após um ano = P0 * (1,03) = P1
População após dois anos = P0 * (1,03)2= P2
População após x anos = P0 * (1,03)x = Px
Vamos supor que a população dobrará em relação ao ano-base após x anos, sendo assim, temos:
Px = 2*P0
P0 * (1,03)x = 2 * P0
1,03x = 2
Aplicando logaritmo
log 1,03x = log 2
x * log 1,03 = log2
x * 0,0128 = 0,3010
x = 0,3010 / 0,0128
x = 23,5
A população dobrará em aproximadamente 23,5 anos.
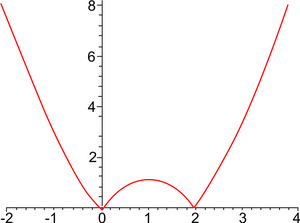
Aplicação da função Modular:
A função modular tem várias aplicações no cotidiano, como por exemplo a aplicação em comparação das temperaturas entre duas ou mais cidade, na Física, na Química na Geografia entre outras.
Exemplo 1 – Geografia
A estrada que liga Recife a Caruaru tem 240 km de extensão e será recuperada em três etapas. Na primeira etapa, será recuperado 1/6 da estrada e na segunda etapa 1/4 da estrada. Quantos quilômetros será recuperada na terceira etapa?
Primeira etapa: 1 / 6
Segunda etapa: 1 / 4
1a + 2a = 1 / 6 + 1 / 4
Efetuando (com mmc)
1a + 2a = 5 / 12
Para completar 12 / 12 ( estrada enteira), falta
12 / 12 - 5 / 12 = 7 / 12
Então, aterceira etapa corresponde a
7 / 12 da estrada



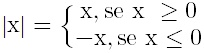




 .
. , sendo que 3 é o logaritmo, 2 é a base e 8 é o logaritmando.
, sendo que 3 é o logaritmo, 2 é a base e 8 é o logaritmando. , sendo que –3 é o logaritmo, 3 é a base e 1/27 é o logaritmando.
, sendo que –3 é o logaritmo, 3 é a base e 1/27 é o logaritmando.








.jpg)




