O módulo de um número é igual a sua distância até zero. Sendo a grandeza distância sempre positiva, conclui-se que o módulo de um número é sempre positivo. Para encontrar o módulo de um número x, por exemplo, siga essa regra prática:
Por exemplo: |6| = 6, pois 6 > 0. Já |– 6| = – (– 6) = 6.
Agora que já relembramos o conceito de módulo, vamos ingressar nas inequações modulares.
Equação modular
De maneira mais formal, podemos definir função modular como:
f(x) = |x| ou y = |x|
A função f(x) = |x| apresenta as seguintes características:
f(x) = x, se x≥ 0
ou
f(x) = – x, se x < 0
Essas características decorrem da definição de módulo.
Exemplo 1. Construa o gráfico da função f(x) = | –x|
Solução: primeiro vamos analisar o gráfico da função acima sem a utilização do módulo na sua lei de formação, ou seja, vamos fazer o gráfico de g(x) = – x

f(x) = |x| ou y = |x|
A função f(x) = |x| apresenta as seguintes características:
f(x) = x, se x≥ 0
ou
f(x) = – x, se x < 0
Essas características decorrem da definição de módulo.
Exemplo 1. Construa o gráfico da função f(x) = | –x|
Solução: primeiro vamos analisar o gráfico da função acima sem a utilização do módulo na sua lei de formação, ou seja, vamos fazer o gráfico de g(x) = – x

O módulo presente na lei da função faz com que a parte do gráfico que se localiza abaixo do eixo x “reflita” no momento em que toca o eixo x. Mas por quê? Simples, a parte do gráfico abaixo do eixo x representa os valores negativos de y e, como o módulo de um número é sempre um valor positivo, o gráfico de f(x) = |– x| fica:

A parte do gráfico que está azul é parte que sofreu ação do módulo.
A parte do gráfico que está azul é parte que sofreu ação do módulo.
Inequação modular
Inequação modular é toda inequação cuja incógnita aparece em módulo. Veja alguns exemplos:
- |x| > 6
- |x| ≤ 4
- |x + 3| > 7
- |4x + 1| ≥ 3
Podemos utilizar as propriedades a seguir para resolver esse tipo de inequação:
- |x| > a → x < – a ou x > a.
- |x| < a → – a < x < a.
- |x| ≤ a → – a ≤ x ≤ a.
- |x| ≥ a → x ≤ – a ou x ≥ a.
- |x – a| ≤ b → – b ≤ x – a ≤ b → a – b ≤ x ≤ a + b
Resolução de inequações modulares
Agora que você já conhece o conceito sobre inequações modulares e suas propriedades resolutivas, é hora de colocar a mão na massa. Antes de analisar as resoluções, tente resolver, utilizando as propriedades explanadas anteriormente, os modelos de inequações modulares acima. Veja as resoluções a seguir:
|x| > 6
x < – 6 ou x > 6
S = {x ∈ R | x < – 6 ou x > 6}
Equação modular
Definição: Equação modular é toda equação cuja incógnita se apresenta em módulo.
Dessa forma, são equações modulares:
- |– 2x + 5| = x
- |3x – 1| = 4
- |10 – 2x| = 2x – 5
Resolução de equações modulares
A resolução de equações modulares baseia-se na definição de módulo, mostrada no início deste texto. 

Vídeo-aula explicativa
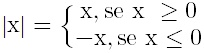
Nenhum comentário:
Postar um comentário